二叉树算法 - 堆和堆的构建
- 1 min数据结构与算法系列(三十七)
什么是堆
堆是一种特殊的二叉树,具备以下特性:
- 堆是一个完全二叉树
- 每个节点的值都必须大于等于(或小于等于)其左右孩子节点的值
如果每个节点的值都大于等于左右孩子节点的值,这样的堆叫大顶堆;如果每个节点的值都小于等于左右孩子节点的值,这样的堆叫小顶堆。
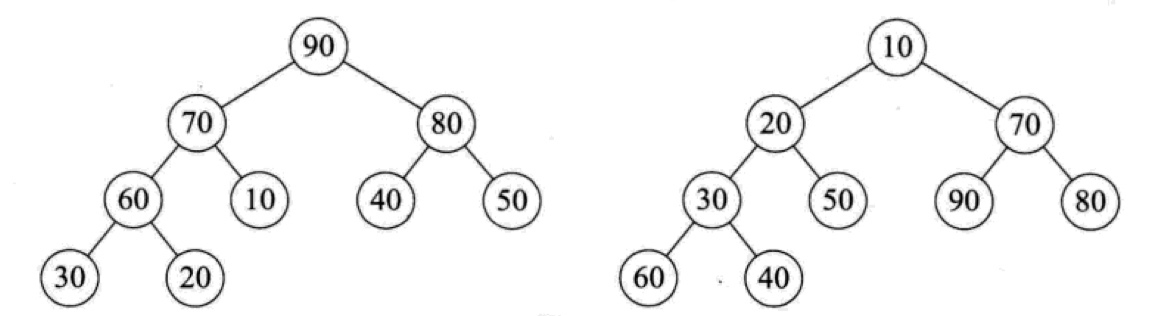
上图中,左侧的堆是大顶堆,右侧的堆是小顶堆,我们还可以得出这个结论:对应大顶堆,堆顶一定是最大值;对于小顶堆,堆顶一定是最小值。
如何构建堆
我们在介绍二叉树的定义和存储的时候说到,由于完全二叉树的特殊性,可以通过数组来存储,堆也是完全二叉树,所以我们可以通过数组来存储它。在使用数组存储堆的时候,把第一个索引位置留空,从第二个索引位置开始存储堆元素,这样,对于索引值为 i 的节点,其子节点索引分别为 2i 和 2i+1。
下面我们就来看如何在堆中插入新节点,以大顶堆为例,从叶子结点插入,如果比父级元素大,则与父级元素交换位置,依次类推,直到到达根节点(小顶堆恰好相反):
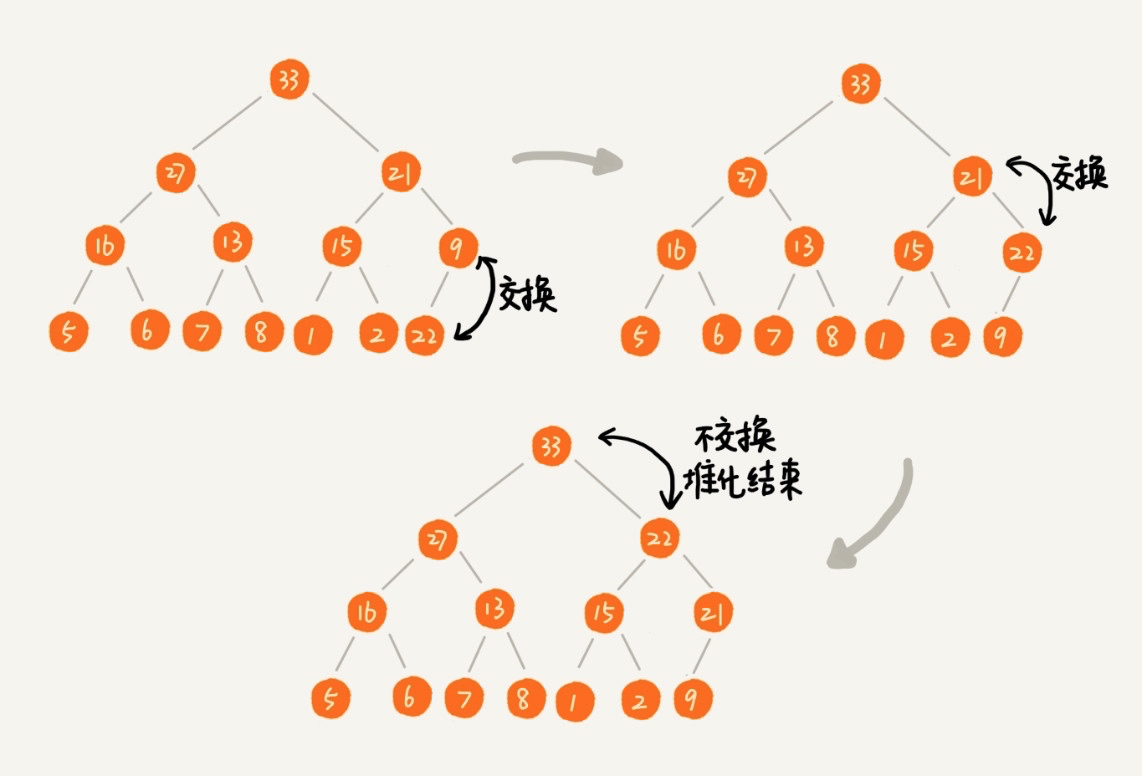
注:构建堆的过程叫堆化。
下面是对应的 PHP 实现代码:
<?php
class Heap
{
private $a = [];
private $n;
private $count;
public function __construct($capacity = 10)
{
$this->n = $capacity;
$this->count = 0;
}
public function insert($data)
{
if ($this->count >= $this->n) {
return false;
}
$this->count++;
$this->a[$this->count] = $data;
$i = $this->count;
while (floor($i/2) > 0 && $this->a[floor($i/2)] < $this->a[$i]) {
$temp = $this->a[$i];
$this->a[$i] = $this->a[floor($i/2)];
$this->a[floor($i/2)] = $temp;
$i = $i / 2;
}
return true;
}
public function __toString()
{
return json_encode(array_values($this->a));
}
}
我们可以为这段代码编写一段测试代码:
$heap = new Heap();
$data = range(1, 10);
shuffle($data);
foreach ($data as $num) {
if (!$heap->insert($num)) {
break;
}
}
print_r($heap);
打印结果如下,符合堆定义,表明堆构建成功:

下一篇我们将来实现如何从堆中删除元素以及堆的使用场景,堆排序的过程其实就是不断从堆中删除最大值(最小值)的过程。