二叉树算法 - 堆排序及其应用
- 1 min数据结构与算法系列(三十八)
堆排序
上篇分享我们介绍了堆的定义及其构建,这篇教程我们来分享堆排序及其应用,堆排序的过程其实就是不断删除堆顶元素的过程。如果构建的是大顶堆,逐一删除后堆顶元素构成的序列是从大到小排序;如果构建的是小顶堆,逐一删除堆顶元素后构成的序列是从小到大排序。而这其中的原理,就是我们在上一篇提到的:对于大顶堆,堆顶一定是最大值;对于小顶堆,堆顶一定是最小值。
但是这里有一个问题,每次从堆顶删除元素后,需要从子节点中取值补齐堆顶,依次类推,直到叶子节点,就会致使存储堆的数组出现「空洞」:
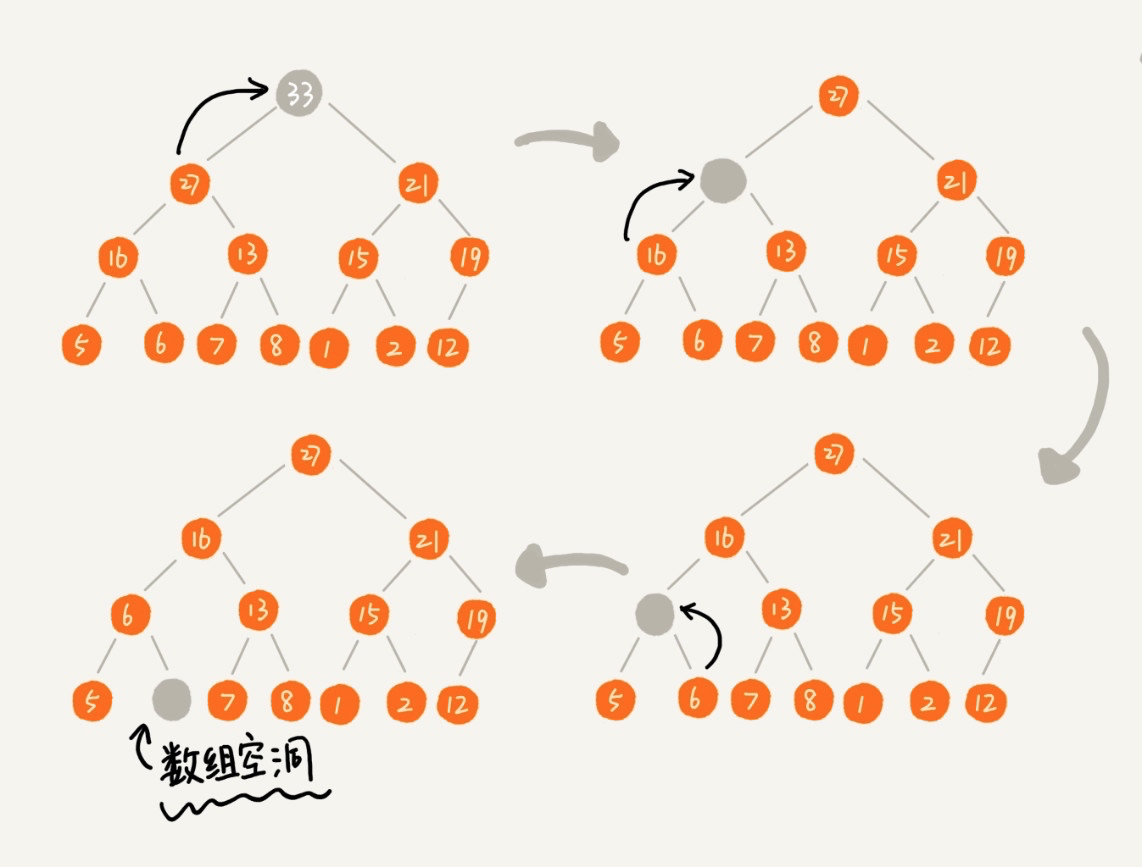
解决办法是将数组中的最后一个元素(最右边的叶子节点)移到堆顶,再重新对其进行堆化:
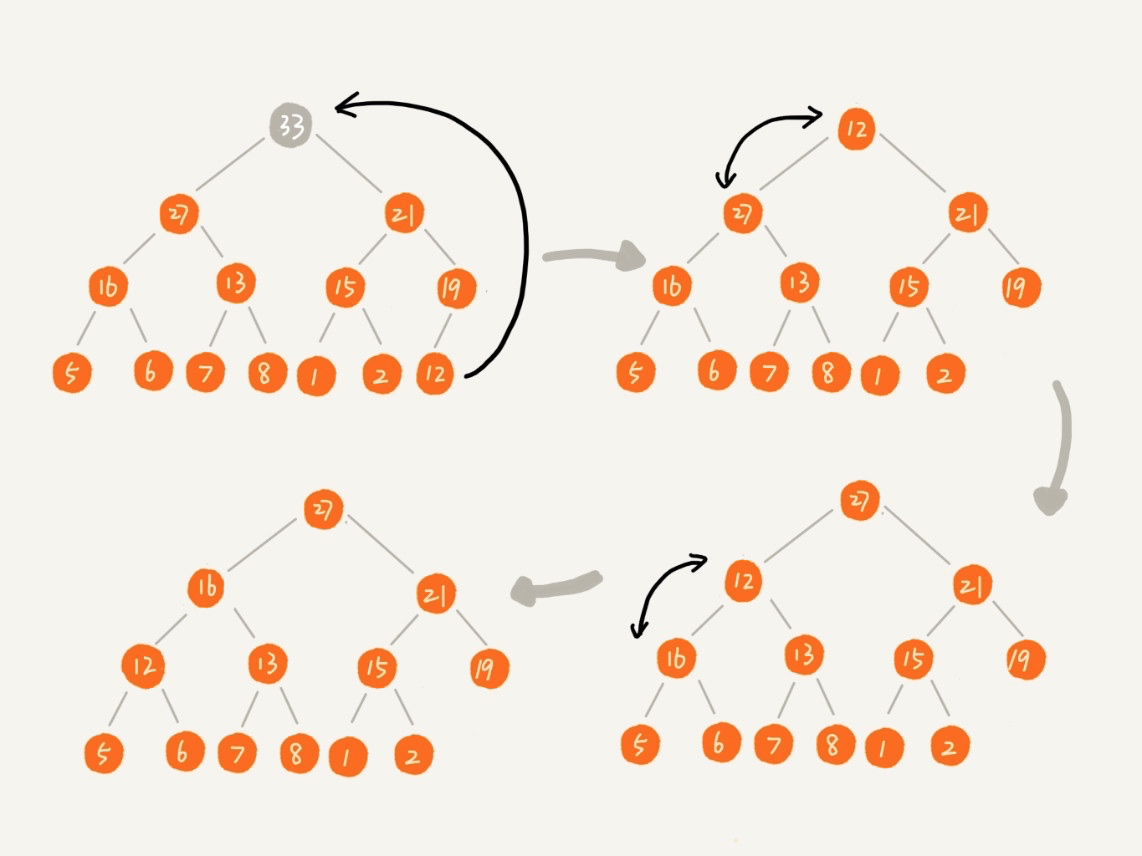
这样,就完美解决了「数组空洞」的问题。
下面我们将堆排序过程转化为对应的 PHP 实现代码如下:
<?php
class Heap
{
private $a = [];
private $n;
private $count;
public function __construct($capacity = 10)
{
$this->n = $capacity;
$this->count = 0;
}
public function insert($data)
{
if ($this->count >= $this->n) {
return false;
}
$this->count++;
$this->a[$this->count] = $data;
$i = $this->count;
while (floor($i/2) > 0 && $this->a[floor($i/2)] < $this->a[$i]) {
$temp = $this->a[$i];
$this->a[$i] = $this->a[floor($i/2)];
$this->a[floor($i/2)] = $temp;
$i = $i / 2;
}
return true;
}
public function remove() {
if ($this->count == 0)
return false;
$removeData = $this->a[1];
$this->a[1] = $this->a[$this->count];
$this->count--;
$i = 1; // 堆顶元素
while (true) {
$maxPos = $i;
if ($i*2 <= $this->count && $this->a[$i*2] > $this->a[$i]) {
$maxPos = 2 * $i;
}
if ($i*2 + 1 <= $this->count && $this->a[$i*2+1] > $this->a[$maxPos]) {
$maxPos = 2 * $i + 1;
}
if ($maxPos == $i) {
break;
}
$temp = $this->a[$i];
$this->a[$i] = $this->a[$maxPos];
$this->a[$maxPos] = $temp;
$i = $maxPos;
}
return $removeData;
}
public function __toString()
{
return json_encode(array_values($this->a));
}
}
我们可以结合堆化和删除方法,写一段测试代码:
$heap = new Heap();
$data = range(1, 10);
shuffle($data);
foreach ($data as $num) {
if (!$heap->insert($num)) {
break;
}
}
$sortedData = [];
while ($removedData = $heap->remove()) {
$sortedData[] = $removedData;
}
print_r($sortedData);
打印的结果如下:
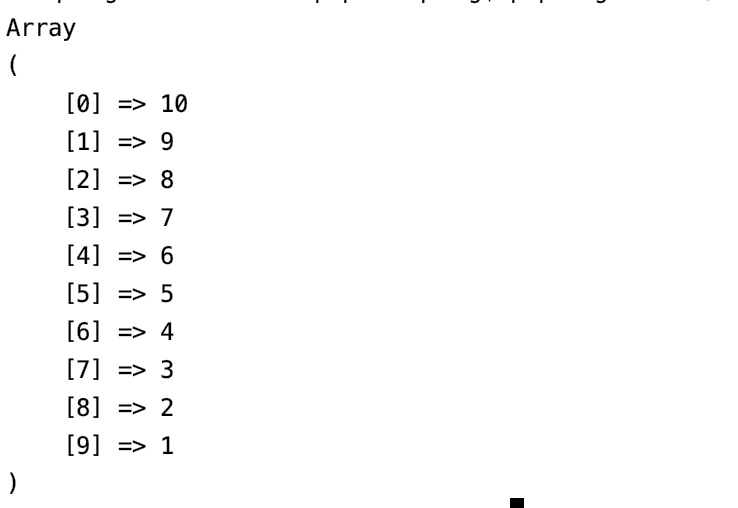
说明堆排序成功,数据变成了从大到小的排序序列。
复杂度分析
我们先看时间复杂度,对堆排序而言,分为两个阶段,一个是堆的构建,一个是堆顶元素的删除。对于 n 个节点的堆化而言,通过数组存储,对应的时间复杂度是 O(n),对于堆顶元素的删除而言,需要遍历 n 个节点,并且,每次删除后需要重新堆化,对应的平均时间复杂度是 O(nlogn)。所以综合下来,堆排序的时间复杂度和快速排序、归并排序一样,是 O(nlogn)。
堆排序的过程中,涉及到不相邻元素的交换(删除堆顶元素的时候),所以不是稳定的排序算法。
我们在删除堆顶元素的时候,使用了额外的存储空间存放被删除的堆顶元素,但是,我们也可以对这个过程进行优化,从而做到原地排序,感兴趣的同学可以试试。
堆排序的应用
- 优先级队列:在优先级队列中,数据的出队顺序不是先进先出,而是按照优先级来,优先级最高的,最先出队,背后的原理就是不断删除堆顶元素。
- 实现TopK排行榜:日常开发中,经常遇到类似求销售额Top10,浏览数Top10,点赞数Top10之类的需求,也可以通过堆排序来实现,原理就是维护一个大小为 K 的小顶堆,有新数据进入后,如果值比堆顶元素大,则删除堆顶元素,最终这个小顶堆就是 TopK 数据了。