二叉树算法 - 赫夫曼编码及压缩算法的简单实现
- 1 min数据结构与算法系列(四十)
上篇文章我们介绍了赫夫曼树的定义和构建,当然,赫夫曼不会闲到为了转化下成绩等级专门实现赫夫曼树,当年,他研究赫夫曼树是为了解决远距离通信(主要是电报)数据传输的最优问题。
比如,我们需要在网络上传输「BADCADEEFD」字符串序列给其他人,每个字符占一个字节,如果要压缩的话可以通过二进制编码的方式进行传输,这个字符串包含了6个字符:ABCDEF,我们可以用对应的二进制表示如下:
| 字符 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 二进制 | 000 | 001 | 010 | 011 | 100 | 101 |
这样,真正传输的数字编码就是「001000011010000011100100101011」,对方接收时按照3位一分来译码,如果文章很长,这个序列串也会非常长。
而事实上,不管是英文还是中文,不同字母或汉字的出现频率是不同的,我们能否参考上篇文章按照成绩区间分布概率不同构建赫夫曼树的方式将这里的字符编码进行优化呢?
答案是可以,具体实现方式如下:
上述「BADCADEEFD」中不同字符的出现大致概率是这样的:
| 字符 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 概率 | 20% | 10% | 10% | 30% | 20% | 10% |
合起来是100%,我们可以这样来构建赫夫曼树(按照上篇文章赫夫曼树构建规则构建):
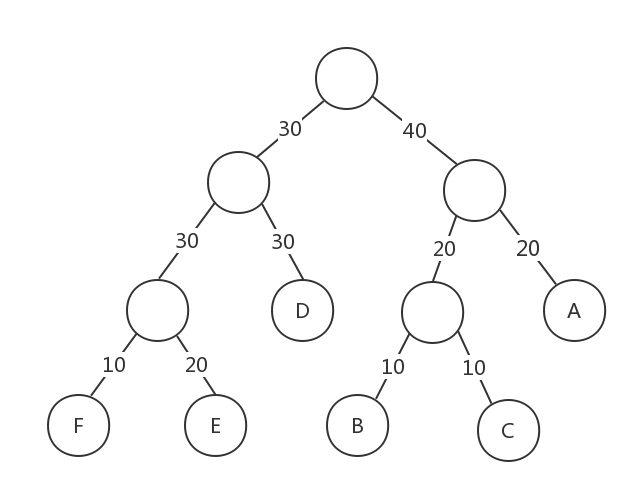

然后我们将权值左分支改为0,右分支改为1,对应的赫夫曼树如下:
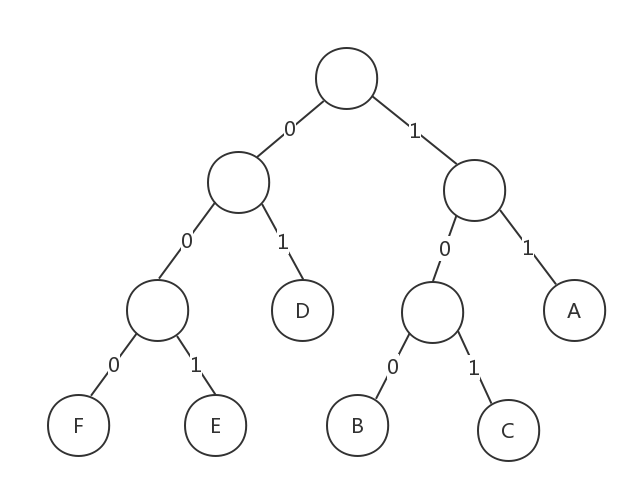
我们按照这六个字母经过路径的权值对字母进行重新编码:
| 字符 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|
| 新编码 | 11 | 100 | 101 | 01 | 001 | 000 |
这样一来我们就得到了新的字符编码,这种编码方式就是赫夫曼编码,我们通过赫夫曼编码对字符串「BADCADEEFD」进行重新编码:
- 原编码二进制串:001000011010000011100100101011(30个字符)
- 新编码二进制串:1001101101110100100100001(25个字符)
这样一来,我们的数据被压缩了,节省了约17%的传输成本,随着字符串长度增加,重复字符增多,效果更明显,并且重复字符越多,压缩效果越好。
最后,在接收方如何解码呢?赫夫曼编码的结果会导致不同字符编码长短不一,很容易混淆,这就要求发送方和接收方约定好同样的编码规则,按照同样的规则进行编码解码,就可以在接收方解析出正确的结果了。就好比二战时期,我方情报人员都要保有同样的密码本一样。