图 - 关键路径的定义及其应用(AOE网)
- 1 min数据结构与算法系列(五十四)
前面介绍的拓扑排序主要是为了解决一个工程是否可以顺利进行的问题,但有时候我们还要解决工程完成需要的最短时间问题。
我们要对一个流程图计算最短时间,就要分析流程之间的拓扑关系,并且找到当中最关键的流程,这个流程的时间就是最短时间。
现在,在前面介绍的 AOV 网的基础上,我们需要引入一个新的概念。在一个表示工程的带权有向图中,用顶点表示事件,用有向边表示活动,用边上的权值表示活动的持续时间,我们把这种通过有向图的边表示活动的网称之为 AOE 网(Activity On Edge Network)。AOE 网中入度为 0 的顶点叫做始点或源点,出度为 0 的点叫做终点或汇点。
一个 AOE 网,总有开始和结束,并且正常情况下,只有一个源点和汇点:
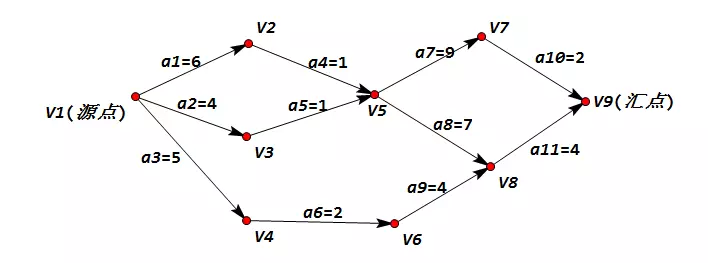
我们把路径上各个活动所持续的时间之和称之为路径长度,从源点到汇点具有最大长度的路径称之为关键路径,在关键路径上的活动叫关键活动。比如上图中,从源点 V1 到汇点 V9 的路径及路径之和是:
- V1->V2->V5->V7->V9:18
- V1->V2->V5->V8->V9:18
- V1->V3->V5->V7->V9:16
- V1->V3->V5->V8->V9:16
- V1->V4->V6->V8->V9:15
所以其关键路径是 V1->V2->V5->V7->V9。
尽管 AOE 网和 AOV 网都是针对工程进行建模的,但是两者有明显的不同,主要体现在 AOV 网是顶点表示活动的网,它只描述活动之间的制约关系;而 AOE 网是边表示活动的网,边上的权值表示活动持续的时间,因此 AOE 网建立在活动之间制约关系没有矛盾的基础之上,再来分析整个工程至少需要多少时间,或者为了缩短完成整个工程所需时间,应当加快哪些活动。这也是 AOE 网的主要应用场景。
下篇文章就来带大家通过数据结构存储 AOE 网,并通过算法实现关键路径的查找。