图 - 关键路径的实现算法和复杂度分析
- 4 mins数据结构与算法系列(五十五)
在上篇文章中简单介绍了关键路径的定义,这篇文章我们来探讨关键路径的实现算法。
在 AOE 网中,某些活动可以并行地进行,因此完成工程的最短时间是从源点到汇点的最大路径长度(事件之间耗时最长的活动完成了,才意味着下个事件可以开始,并行的活动并不是可选的,而是都要执行的,这一点需要明确),而找到这条具有最大路径长度的路径,也就找到了关键路径。
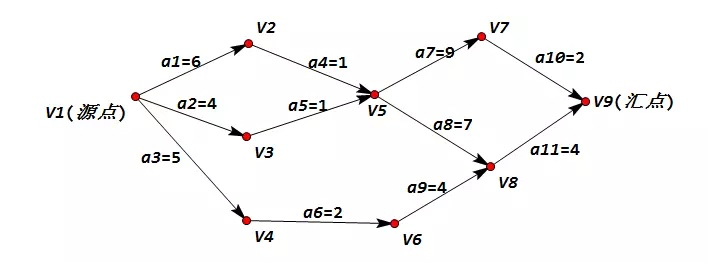
比如上篇引用的这个示例 AOE 网,其关键路径是 V1->V2->V5->V7->V9。
下面我们来探讨如何用抽象的算法来寻找关键路径,为了方便描述这个算法,需要先定义几个变量:
\1. 事件的最早发生时间 etv,即顶点 Vk 的最早发生时间;
\2. 事件的最晚发生时间 ltv,即顶点 Vk 的最晚发生时间,超出这个时间就会导致整个工程延期;
\3. 活动的最早开始时间 ete,即弧 ak 的最早开始时间;
\4. 活动的最晚开始时间 lte,即弧 ak 的最晚开始时间,也就是不会导致工程延期的最晚开始时间。
要找到关键路径,需要找到所有活动的最早开始时间和最晚开始时间,并且比较它们,如果相等则意味着此活动是关键活动(即弧的权值代表时间被填满),活动间的路径是关键路径,否则不是。
在上面几个变量中,通过 1、2 可以推导出 3、4,所以,通过 etv[k] 与 ltv[k] 是否相等即可判断 ak 是否是关键活动,对应的路径是否是关键路径。
下面,我们通过代码来实现上述算法。由于 AOE 网基于 AOV 网之上,只是弧上有权值,所以完全可以基于在拓扑排序中定义的数据结构 DirectedWeightedGraph 类来实现 AOE 网的存储,并且计算所有顶点 etv 的过程,就是对 AOE 网从头到尾进行拓扑排序的过程,只是需要对代码略微做一些调整。
首先需要为 DirectedWeightedGraph 类新增几个属性:
protected $etv = []; // 存储所有顶点最早开始时间
protected $ltv = []; // 存储所有顶点最晚开始时间
然后修改拓扑排序实现方法 topologicalSort 代码如下:
/**
* 拓扑排序
* @return array|bool
*/
public function topologicalSort()
{
$stack = []; // 存放入度为零的顶点(以栈的方式实现)
$count = 0; // 统计输出顶点数
$sorted = []; // 存储拓扑排序结果
foreach ($this->vData as $pos => $data) {
$vertex = $this->getVertex($pos);
if ($vertex && $vertex->in == 0) {
$stack[] = $pos;
}
$this->etv[$pos] = 0; // 初始化 etv
}
while ($stack) {
$start = array_pop($stack); // 开始顶点
$sorted[] = $start;
$vertex = $this->getVertex($start);
$count++;
$eNode = $vertex->next;
while ($eNode) {
$k = $eNode->data; // 与起点相邻的顶点
$oVertex = $this->getVertex($k);
if (!(--$oVertex->in)) { // 「删除」该弧,将对应顶点入度值减1
$stack[] = $k; // 若为0则入栈,以便下次循环输出
}
// 求各顶点(事件)最早发生时间
if ($this->etv[$start] + $eNode->weight > $this->etv[$k]) {
$this->etv[$k] = $this->etv[$start] + $eNode->weight;
}
$eNode = $eNode->next;
}
}
if ($count < $this->vNum) {
return false; // 存在环
}
return $sorted;
}
有了拓扑排序结果和 etv 数据后,我们接下来来实现关键路径算法,在 DirectedWeightedGraph 类中新增一个 criticalPath 方法:
/**
* 关键路径
*/
public function criticalPath()
{
$sorted = $this->topologicalSort();
for ($i = 0; $i < $this->vNum; $i++) {
$this->ltv[$i] = $this->etv[$this->vNum - 1]; // 初始化 ltv
}
while ($sorted) {
$start = array_pop($sorted);
$vertex = $this->getVertex($start);
$eNode = $vertex->next;
while ($eNode) {
$k = $eNode->data;
// 求各顶点(事件)最晚发生时间
if ($this->ltv[$k] - $eNode->weight < $this->ltv[$start]) {
$this->ltv[$start] = $this->ltv[$k] - $eNode->weight;
}
$eNode = $eNode->next;
}
}
for ($i = 0; $i < $this->vNum; $i++) {
$vNode = $this->getVertex($i);
$eNode = $vNode->next;
while ($eNode) {
$k = $eNode->data;
$ete = $this->etv[$i];
$lte = $this->ltv[$k] - $eNode->weight;
if ($ete == $lte) {
printf("<V%s, V%s> length: %d , ",
$vNode->data, $this->vData[$eNode->data], $eNode->weight);
}
$eNode = $eNode->next;
}
}
}
分析整个关键路径的算法,对于有 n 个顶点和 e 条弧的 AOE 网而言,拓扑排序的时间复杂度是 O(n+e),计算事件最晚发生时间事件复杂度也是 O(n+e),最后计算关键路路径的时间复杂度还是 O(n+e),所以整体的时间复杂度依然是 O(n+e)。