图 - 图的存储
- 1 min数据结构与算法系列(四十四)
由于图这种数据结构比较复杂,单纯的数组和链表已经无法表示了,需要通过更复杂的结构来存储。
今天,简单为大家介绍两种存储图的方式,一种是基于数组,一种是基于链表,但是不是简单的数组和链表,下面我们就一起来看看到底是如何存储图的。
邻接矩阵
显然,通过一维数组是无法存储图的,因为图包含顶点和边,而且每个顶点都可能与其他顶点有关联,所以我们通过两个数组来存储图:一个一维数组用于存储所有顶点,一个二维数组来存储连接顶点的边/弧,边或弧连接的是两个顶点,所以需要二维数组来存储。我们把这种存储图的方式叫做邻接矩阵。
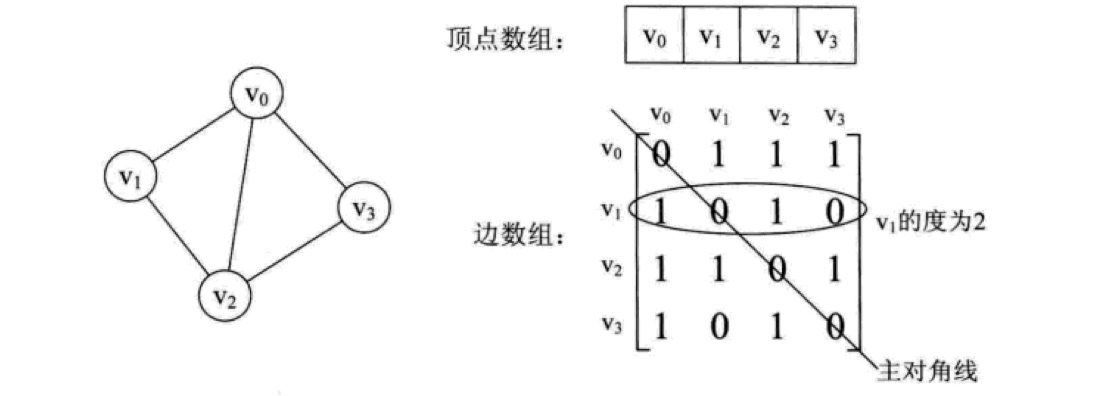
说概念很抽象,下面我们通过实例来演示,对于无向图而言,由于边没有方向,所以存储无向图边的二维数组是一个对称矩阵(矩阵是一个数学概念,一个 m x n 的矩阵是一个由 m 行 n 列元素排列成的矩形阵列):
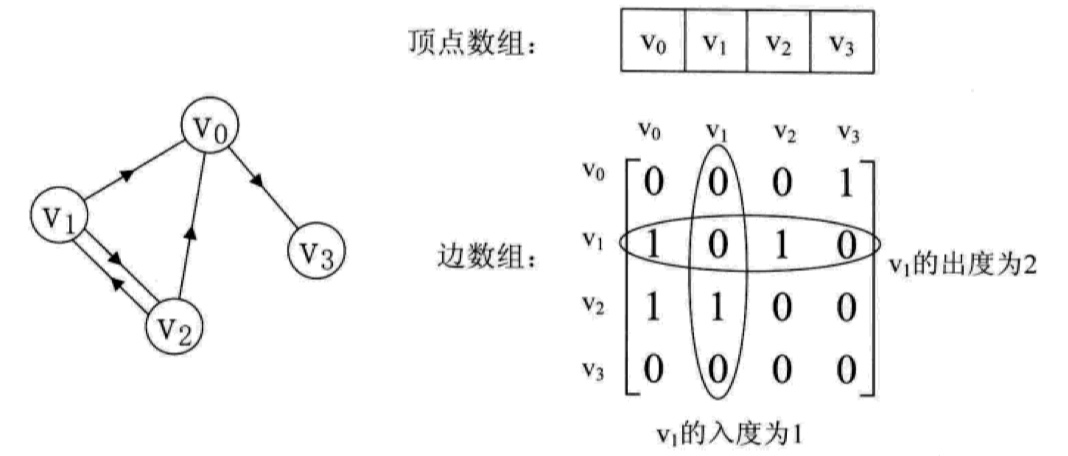
对于有向图而言,由于边是有方向的,我们将二维数组中指向某个顶点的元素值设置为1,否则设置为0,比如下面 v1v0 为 1,而 v0v1 为 0(注意存储顺序,先横后纵,横向表示某个顶点的出度,纵向表示某个顶点的入度):
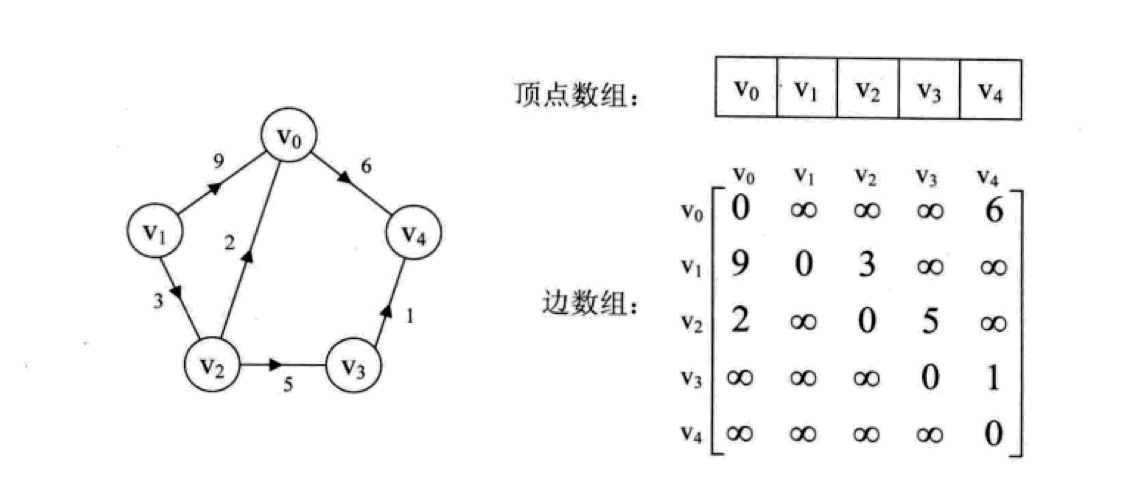
对于带权的有向图,要更复杂一些,在存储弧的二维数组中,相邻的顶点对应元素值等于权重(入度),自己指向自己的对应元素值为0,否则等于无穷大(∞):
对于邻接矩阵而言,初始化的时间复杂度等于边数组构建的复杂度,对于有 n 个顶点的图而言,时间复杂度是 O(n^2),空间复杂度也是如此,而且如果图比较稀疏的话(稀疏图),边数组会存在巨大的空间浪费。但是优点是实现起来非常简单,对于稠密图或者非常简单的图来说,用邻接矩阵是比较方便的。
邻接表
既然稀疏图用邻接矩阵存储不合适,那要怎么存储呢?有了前面的数据结构基础,我们很容易会联想到基于链表替代边数组来存储边,这样就可以避免对空间的浪费了。这种存储方式还是通过一个一维数组来存储顶点,只是将边/弧通过链表来表示,我们把这种存储方式叫做邻接表。
对于无向图来说,通过邻接表来存储,可以这么实现:
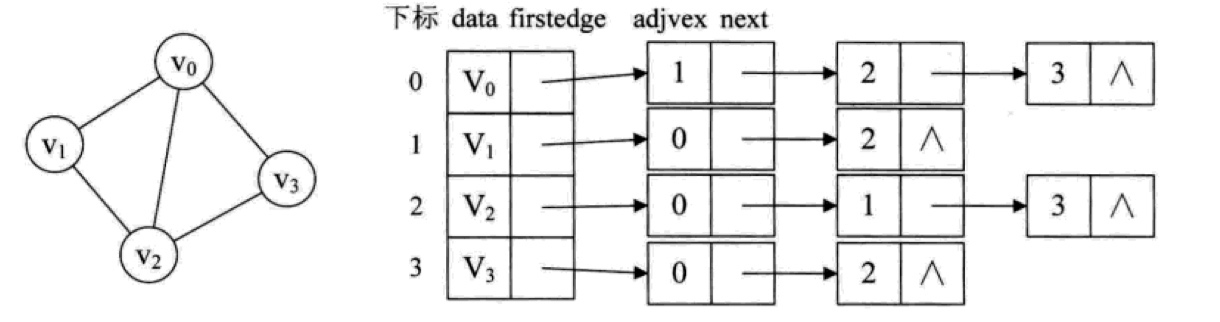
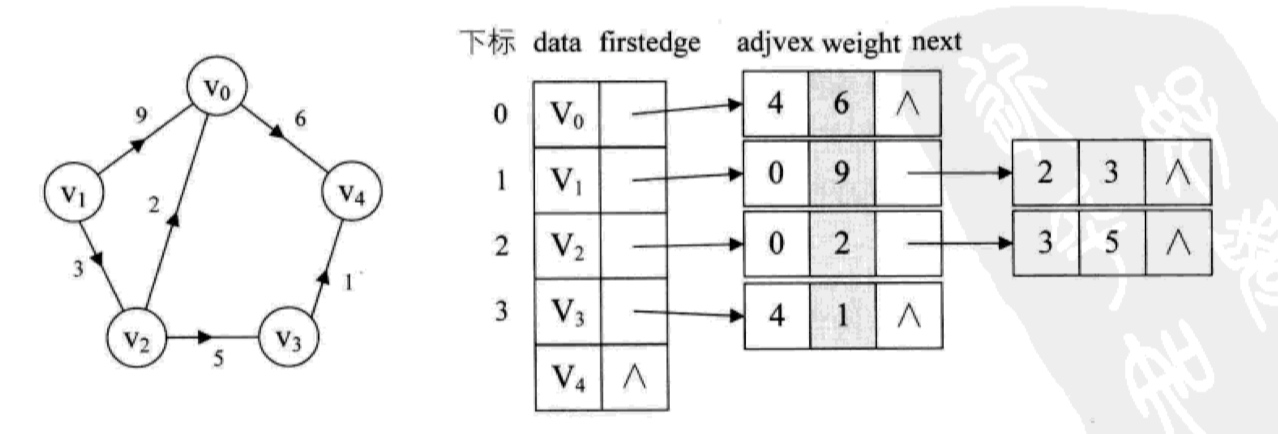
我们在每个顶点上通过 data 保存数据,通过 firstedge 指向第一个邻接顶点,指向节点上 adjvex 存储的是对应顶点的数组下标,如果该顶点有多个邻接顶点,可以通过 next 指向下一个邻接顶点,如果没有的话,则将对应指针设置为空。
对于有向图来说,原理也是类似,只不过有向图的边有方向而已,链表指针指向基于出度,所以很容易计算出某个顶点的出度:
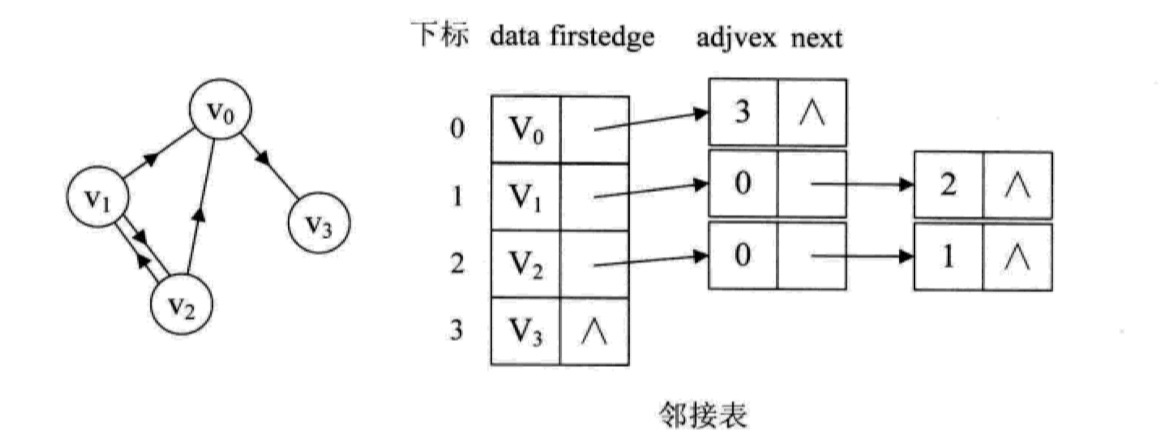
显然,邻接表的构建时间复杂度要比邻接矩阵好,对于一个有 n 个顶点和 e 条边的图而言,时间复杂度是 O(n+e),而且不存在任何空间的浪费,比较高效,可用于存储任何图。
但邻接表也不是十全十美,对于有向图来说,如果要计算某个顶点的入度,需要遍历整个图才能实现,要解决这个问题,我们可以通过逆邻接表来实现。所谓逆邻接表,就是和邻接表相反,指针指向基于入度,这样我们就可以很轻松计算某个顶点的入度了。比如上面那个有向图,我们可以这样通过逆邻接表来构建:
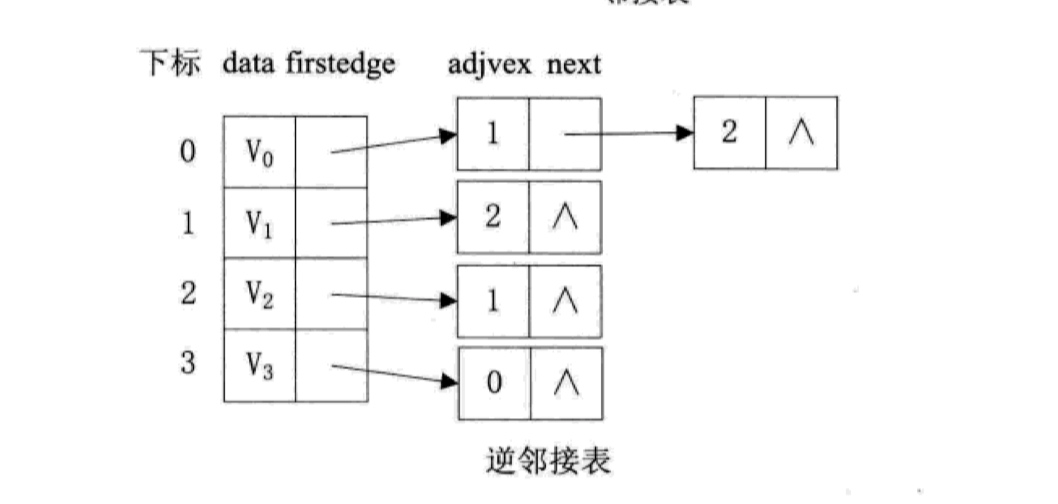
对于有权重的有向图(网图),还要通过一个额外的 weight 域来存储权重: