图 - 图的相关概念
- 1 min数据结构与算法系列(四十三)
今天开始,我们来介绍最后一个也是最复杂的一个数据结构 —— 图。图会综合运用前面所介绍的所有数据结构,所以说,学好了图,也就等同于掌握了数据结构的精髓。
图的基本定义
图(Graph)由顶点(Vertex)和边(Edge)组成。图中的元素叫顶点,图不能为空,在线性表中,相邻元素有前后关系,在树中,相邻元素有层次关系,在图中,任意两个元素之间都可能有关系,顶点之间的关系通过边来表示。图可以表示为 G(V,E),其中 G 表示图,V 表示顶点的集合,E 表示边的集合。
下面就是一个典型的图:
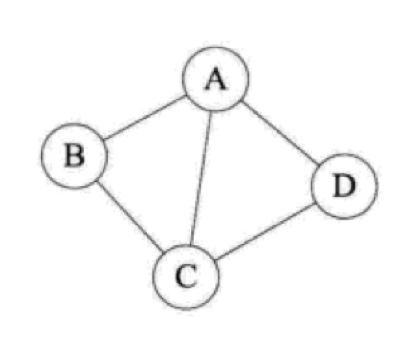
其中字母标识的节点就是图的顶点,节点之间的连线就是图的边。
无向图与有向图
没有方向的边叫无向边,任意两个顶点之间都是无向边的图叫无向图,比如上面那个示例图就是无向图。在无向图中,任意两个顶点之间都有边的图叫无向完全图。
与之相对的,有方向的边叫有向边(也叫弧),任意两个顶点之间都是有向边的图叫有向图,例如下面这个图就是有向图:
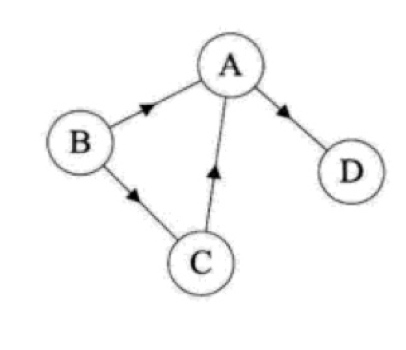
在有向图中,任意两个顶点之间都有方向相反的两条有向边的图叫有向完全图。
按照边的数目,我们将边数很少的图叫稀疏图,边数很多的图叫稠密图。
有些图的边还拥有与其相关的数字,我们把这个数字叫做权,这种带权的图通常称作网。
顶点与边的关系
顶点的度指的是与顶点相连接的边数,整个图的度数是所有顶点度数之和。
在无向图中,边不分方向,边数是图的度数/2。
在有向图中,边有方向,按照方向将有向图顶点的度分为出度和入度,出度表示有多少条边是以这个顶点为起点指向其他顶点;入度表示有多少条边指向这个顶点。
在树中,顶点到任意节点的路径是唯一的,而在图中,顶点到任意顶点的路径却不是唯一的。比如上述示例有向图中,从 B 到 A 就有 B->A、B->C->A 两条路径,示例无向图中还有 B->C->D->A 这条路径。
连通图
在无向图 G 中,如果顶点 v 到顶点 v’ 有路径,则称 v 和 v’ 是连通的,如果任意两个顶点都是连通的,则称 G 是连通图。比如上述示例无向图就是连通图。
在有向图 G 中,对于每一对顶点,如果相互之间都存在路径,则 G 是强连通图。上述示例有向图不是强连通图,因为 A 到 D 存在路径,而 D 到 A 不存在。
图的应用场景
图的应用场景很多,比如社交网络中用户之间的关系,网络设备之间的拓扑结构,以及现实生活中形形色色的网:公路网、铁路网、地铁网等,都可以通过图来表示。