图 - 图的遍历(上)—— 深度优先搜索
- 6 mins数据结构与算法系列(四十五)
前面我们已经介绍了图的定义和存储,今天这篇我们来探讨图的遍历,图的遍历和树的遍历类似,最直接的理解就是,在图中某个顶点出发,访遍图中其余顶点,并且其中每个顶点仅被访问一次,这个过程就是图的遍历。
图的遍历主要有两种方式,一种是深度优先搜索,一种是广度优先搜索。我们先来看深度优先搜索。
深度优先搜索定义
深度优先搜索(Depth First Search),简称DFS,这种算法有点像走迷宫,沿着一条路径一直走,如果某个路径不通,则回到前驱节点,以此为出发点继续尝试下一条路径,以此类推,直到访遍所有顶点。
深度优先搜索也是这样,它从图的某个顶点出发,访问此顶点,然后从该顶点未被访问的邻接顶点出发,深度遍历图,在未遇到已访问过的重复顶点前,我们约定右手优先原则,一直往前走,遇到已经访问过的顶点,则回溯到前驱顶点,访问与其相邻路径对应的邻接顶点,继续做上述判断,依次类推,直到图中所有与该顶点路径想通的顶点都被访问到,如下图所示:
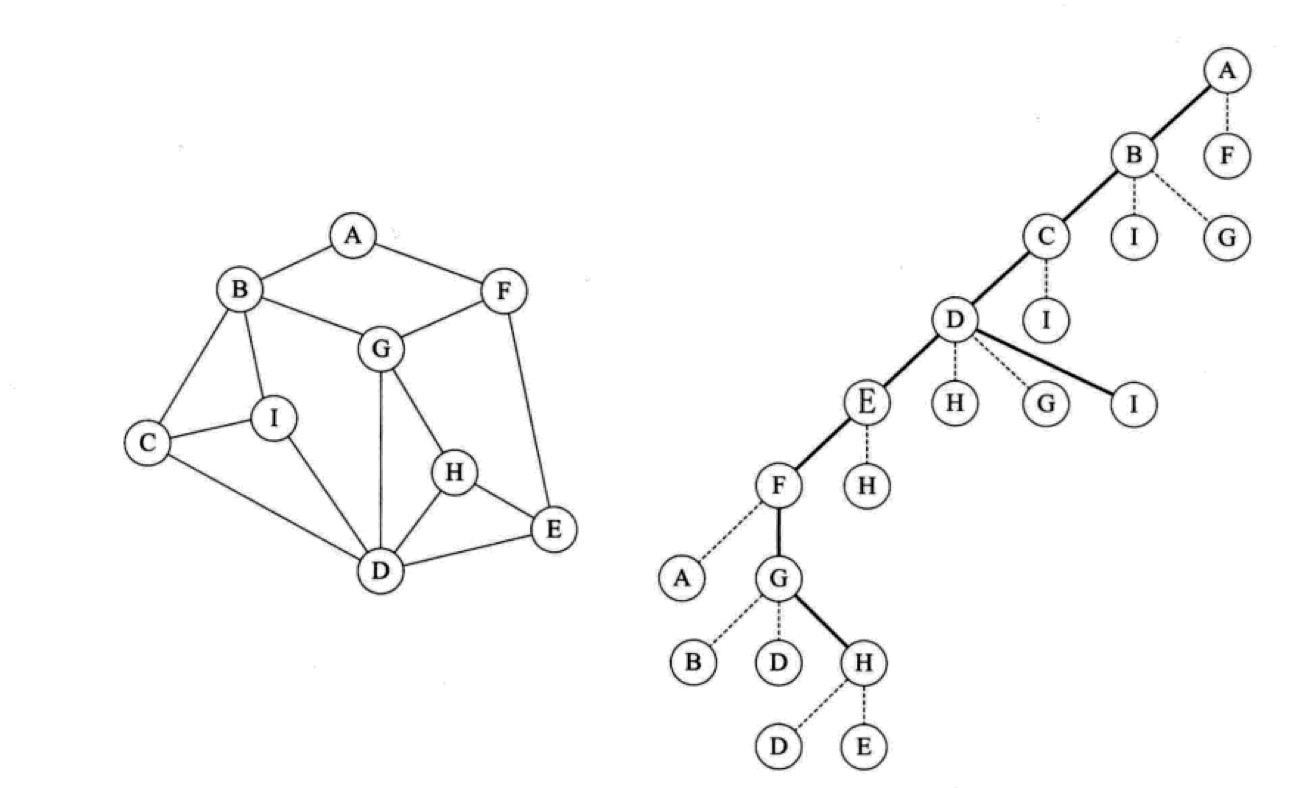
如果还有顶点未被访问,则将其作为起点,重复上述过程,直到图中所有顶点都被访问到。
下面我们用代码来实现这个过程。
通过邻接表实现图的存储
在实现深度优先搜索之前,我们先定义一个数据结构来存储图,这里我们采用邻接表的方式。
为此要创建链表类 LinkedList 及对应的节点类 Node:
/**
* Class Node
* 链表节点类
*/
class Node
{
public $data;
/**
* @var Node
*/
public $next;
public function __construct($data = null)
{
$this->data = $data;
}
}
/**
* Class LinkedList
* 链表类
*/
class LinkedList
{
private $head = null;
private $count = 0;
public function __construct()
{
$emptyNode = new Node();
$this->head = $emptyNode;
}
public function insert($data)
{
if ($this->head == null) {
return;
}
$newNode = new Node($data);
$newNode->next = $this->head->next;
$this->head->next = $newNode;
$this->count++;
}
public function remove(Node $node)
{
if ($node == null) {
return false;
}
$preNode = $this->pre($node);
$preNode->next = $node->next;
$this->count--;
}
public function get($index)
{
if ($index >= $this->count) {
return false;
}
$node = $this->head->next;
$i = 0;
while ($node) {
if ($i == $index) {
return $node;
} else {
$node = $node->next;
$i++;
}
}
return false;
}
public function pre(Node $node)
{
if ($node == null) {
return false;
}
$preNode = $this->head;
$curNode = $this->head->next;
while ($curNode) {
if ($curNode === $node) {
return $preNode;
} else {
$preNode = $curNode;
$curNode = $preNode->next;
}
}
return false;
}
public function getSize()
{
return $this->count;
}
public function __toString()
{
$node = $this->head->next;
$arr = [];
$i = 0;
while ($node) {
$arr[] = 'Node[' . $i . ']:data=>' . $node->data . ',next=>' . json_encode($node->next);
$i++;
$node = $node->next;
}
return implode("\n", $arr);
}
}
然后我们来定义一个 Graph 类通过邻接表来存储图:
/**
* Class Graph
* 通过邻接表存储图
*/
class Graph
{
private $v; # 顶点个数
/**
* @var LinkedList[]
*/
private $adj = []; # 邻接表
private $found = false;
public function __construct(int $v)
{
$this->v = $v;
for ($i = 0; $i < $v; $i++) {
$this->adj[$i] = new LinkedList();
}
}
// 无向图同一条边要存两次
public function addEdge($s, $t)
{
$this->adj[$s] = $t;
$this->adj[$t] = $s;
}
}
我们首先将所有顶点的邻接顶点设置为空链表,然后我们可以通过 addEdge 方法为图添加边($s 和 $t 分别代表边的两个顶点),从而完成图的构建。
有了完整的图之后,就可以编写深度优先搜索方法对其进行遍历了。
通过PHP代码实现深度优先搜索
我们在 Graph 类中定义深度优先搜索方法 dfs 如下:
public function dfs($s, $t)
{
$this->found = false;
for ($i = 0; $i <= $this->v; $i++) {
$visited[$i] = 0;
}
for ($i = 0; $i <= $this->v; $i++) {
$prev[$i] = -1;
}
$this->recurDfs($s, $t, $visited, $prev);
$this->printPath($prev, $s, $t);
}
public function recurDfs($w, $t, $visited, $prev)
{
if ($this->found == true) {
return;
}
$visited[$w] = 1;
if ($w == $t) {
$this->found = true;
return true;
}
for ($i = 0; $i < $this->adj[$w]->getSize(); $i++) {
$q = $this->adj[$w]->get($i)->data;
if (!$visited[$q]) {
$prev[$q] = $w;
$this->recurDfs($q, $t, $visited, $prev);
}
}
}
public function printPath($prev, $s, $t)
{
if ($prev[$t] != -1 && $t != $s) {
$this->printPath($prev, $s, $prev[$t]);
}
print $t;
}
我们先将每个顶点是否已经访问设置为 0,将每个顶点的前驱节点设置为 -1,然后通过一个递归方法 recurDfs 实现深度优先搜索算法,如果最终起点与终点重合则表示两个顶点之间的所有顶点已经遍历完毕,立即返回,否则继续搜索。
搜索完毕后,将路径信息通过 printPath 打印出来。这个测试任务交给你们自己去完成。
深度优先搜索的时间复杂度很显然是 O(v+e),其中 v 表示顶点数,e 表示边数,需要额外的数组存储已访问顶点和前驱顶点,对应的空间复杂度是 O(v)。