图 - 拓扑排序的定义及其应用场景
- 1 min数据结构与算法系列(五十二)
前面介绍的最小生成树和最短路径都是有环图的应用,接下来我们来介绍无环图的应用,所谓无环图,就是图中没有回路。无环图两个常见的应用就是拓扑排序和关键路径。
我们先来看看拓扑排序。
在日常生活中,我们通常会把软件开发、生产流程、网络设备互联都当成一个项目工程来对待,所有工程都可以分为若干个子工程(或者称之为「活动」),这些子工程之间往往会有一些条件约束,比如其中某些活动必须在另一些活动完成之后才能进行。下面是一个简单的软件开发流程图:
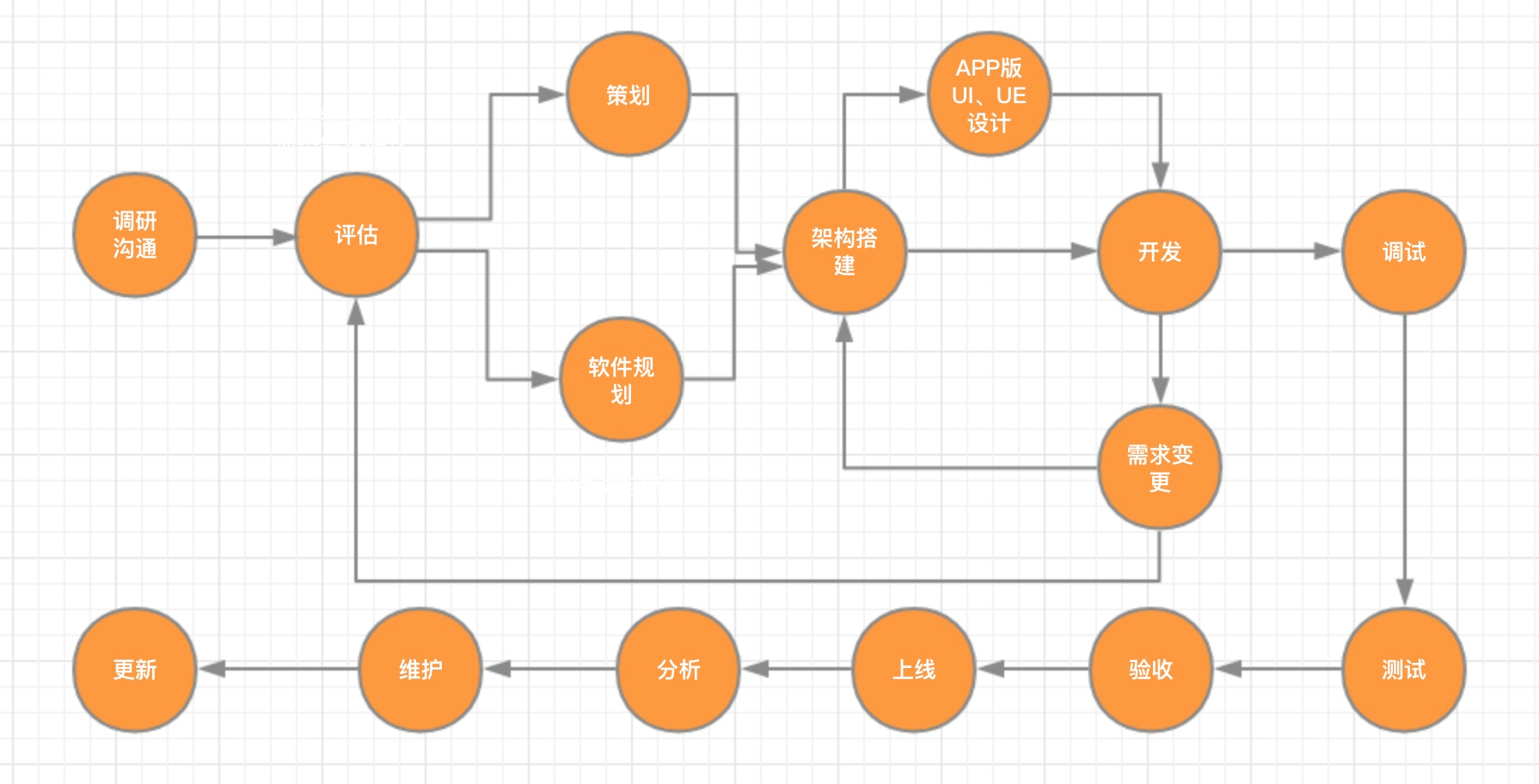
我们将整个流程抽象为图这种数据结构,则每个子工程节点就是图的顶点,连接子工程的前后约束就是图的边(并且是有方向的边),并且工程有起始节点,也有结束节点,并且,首尾不会相连,所以综合来看,这样的工程图,一定是无环的有向图。
在一个表示工程的有向图中,用顶点表示活动,用弧(有方向的边)表示活动之间的优先关系,这样的以顶点表示活动的有向图,我们称之为 AOV 网(Activity On Vertex Network)。
有了以上的准备工作,下面我们正式介绍拓扑排序的概念。
设 G=(V,E)(其中V表示顶点集合,E表示弧集合)是一个具有 n 个顶点的有向图,V 集合中的顶点满足从顶点 i 到顶点 j 之间有一条路径,并且在顶点序列中 i 一定在 j 之前,则我们称这样的序列为一个拓扑序列。
而所谓的拓扑排序,就是对有向图构造拓扑序列的过程。
构造结果中如果全部顶点都被输出,则说明它是不存在回路的 AOV 网;否则说明存在回路,不是 AOV 网。
对于不存在回路的 AOV 网,可以应用在各种不同的工程或项目流程图中,满足各种场景的需要,所以拓扑排序在工程中非常有实用价值。
下一篇,就来给大家介绍如何实现拓扑排序算法。