图 - 最小生成树的定义和应用场景
- 1 min数据结构与算法系列(四十七)
我们前面在介绍图的相关概念的时候,提到过连通图,以无向图为例,如果图的任意两个顶点之间都是想通的,这个图就是连通图,今天我们在此基础上进一步介绍连通图的生成树概念。
一个连通图的生成树是一个极小的连通子图,它含有图中全部的 n 个顶点,和足以构成一棵树的 n-1 条边,如下图所示:
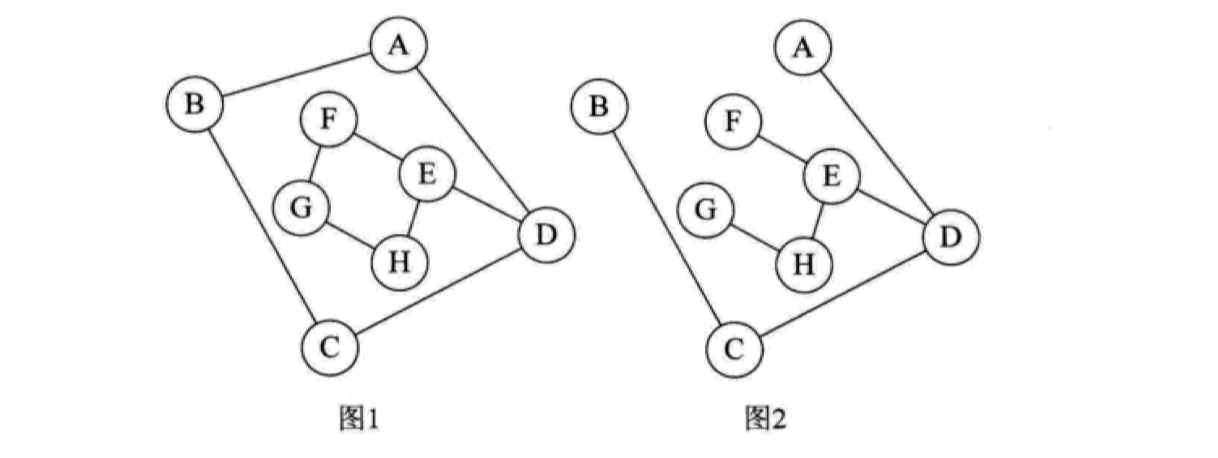
图1是一个连通图,图2是该连通图的生成树,反过来说,如果一棵树大于 n-1 条边,则必然构成环。
前面我们也提到,带权的图叫做网,我们把构造连通网(带权连通图)的最小代价生成树叫做最小生成树。这个最小代价指的是通过 n-1 条边具有把 n 个顶点的连通图连接起来,并且使所有边的权值和最小。如下图所示,实线部分就是最小生成树:
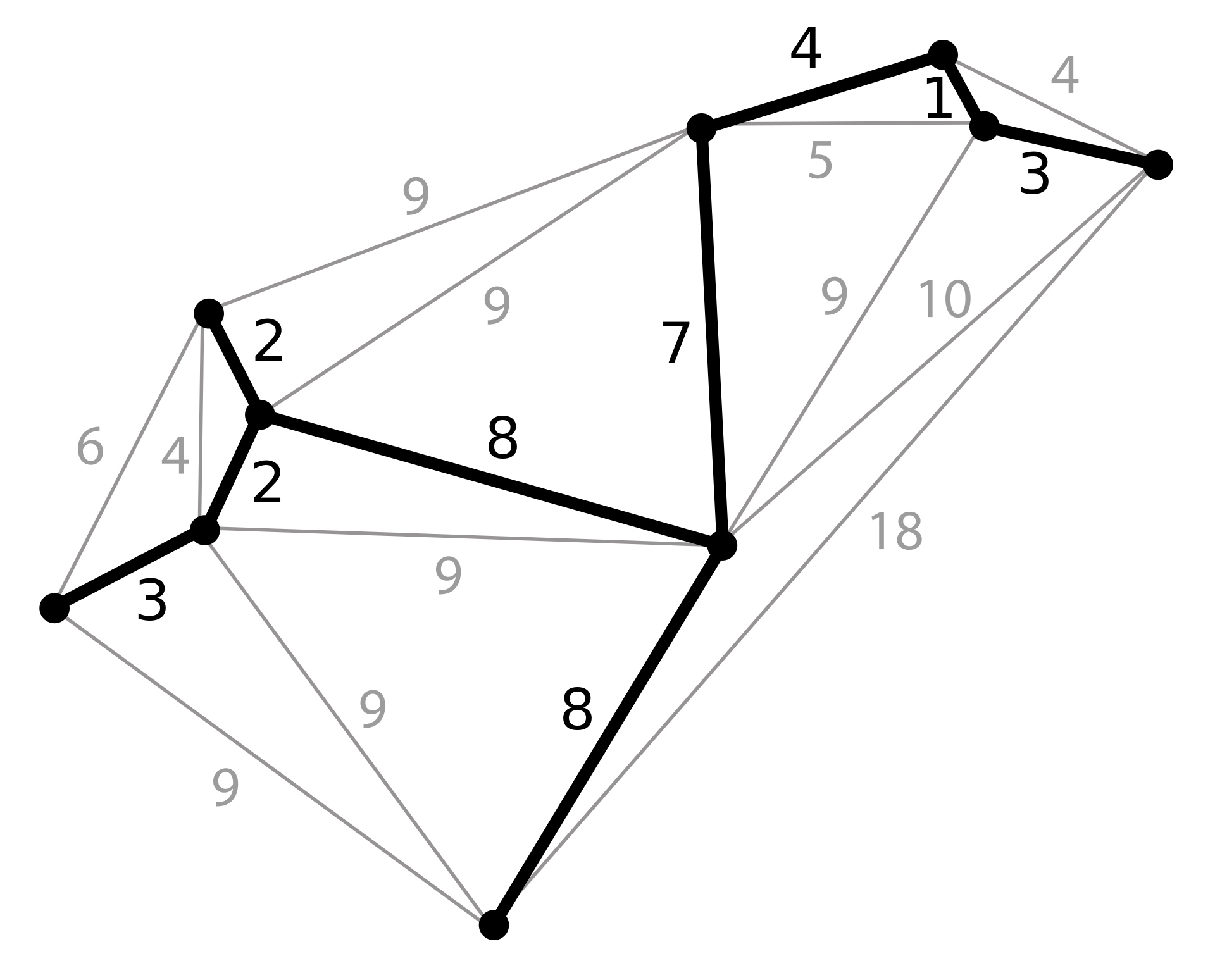
最小生成树的应用场景很多,小到我们要来个欧洲十国游,怎么规划路径让交通费用最低,大到国家的电力网、公路网、通信网,怎么规划路径可以让建设成本最低,学习了最小生成树后,你就可以通过算法来计算出最佳路径了,不仅如此,所有涉及连接网络中所有节点的最优路径问题,都可以通过最小生成树来处理。
最小生成树有多种实现算法,我们这里介绍两种比较常见的:普里姆算法(Prim)和克鲁斯卡尔算法(Kruskal)。下一篇我们将演示这两个算法的实现和并进行复杂度分析。