图 - 最小生成树的实现算法之克鲁斯卡尔(Kruskal)算法
- 1 min数据结构与算法系列(四十九)
上篇文章我们分享了通过普里姆算法实现最小生成树,该算法主要以顶点为维度,时间复杂度也只与顶点相关,今天我们要给大家介绍最小生成树的另一种实现算法 —— 克鲁斯卡尔(Kruskal)算法。
原理
与普里姆算法不同,克鲁斯卡尔算法主要以边为维度,每次从剩下的边中找权重值最小的边来构建最小生成树,具体实现思路如下:
- 将无向图的边按权重大小递增式排序,放到集合中
- 遍历该集合,找出权重最小的边,加入到结果生成树的集合中
- 如果结果生成树出现回路,则放弃这条边
- 重新执行步骤2,直至所有顶点被遍历,最终生成最小生成树
该实现原理图示如下:
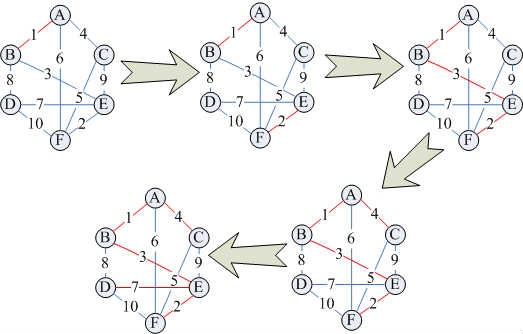
实现
我们继续在上篇文章创建的 EdgeWeightedGraph 类中编写克鲁斯卡尔算法实现方法,按照克鲁斯卡尔算法实现原理,需要构建无向图的边集合,我们在 EdgeWeightedGraph 类中新增一个边集合属性:
/**
* @var Edge[]
*/
private $edges = []; // 边数组
然后在添加边的时候顺便将其添加到边集合数组中:
// 添加边
public function addEdge($s, $t, $weight)
{
$esNode = new ENode($s, $weight);
$etNode = new ENode($t, $weight);
$this->adj[$s]->insertENode($etNode);
$this->adj[$t]->insertENode($esNode);
$this->edges[] = new Edge($s, $t, $weight);
$this->edges[] = new Edge($t, $s, $weight);
}
定义好数据结构之后,我们编写 Kruskal 算法实现代码如下:
public function kruskal()
{
// 按照权重值大小对边数组进行排序(升序)
usort($this->edges, function ($edge, $anotherEdge) {
if ($edge->weight < $anotherEdge->weight) {
return -1;
} elseif ($edge->weight > $anotherEdge->weight) {
return 1;
} else {
return 0;
}
});
$kruskalTree = []; // 最小生成树
$parent = []; // 存储前驱顶点,用于判断回路
$points = [];
$sum = 0; // 总权值
foreach ($this->edges as $edge) {
// 如果存在回路则跳过
if (!$this->isLoop($parent, $edge->start, $edge->end)) {
$points[] = $edge->start;
$points[] = $edge->end;
// 边数校验
if (count($kruskalTree) + 1 > count(array_unique($points)) - 1) {
continue;
}
$parent[$edge->start] = $edge->end;
$kruskalTree[] = $edge;
$sum += $edge->weight;
// n-1 条边
if (count($kruskalTree) == $this->vNum - 1) {
break;
}
}
}
// 打印最小生成树
printf("KRUSKAL()=%d: ", $sum);
foreach ($kruskalTree as $edge) {
printf("(%s,%s): %d\n", $this->vData[$edge->start], $this->vData[$edge->end], $edge->weight);
}
}
// 判断是否存在回路
protected function isLoop($parent, $start, $end)
{
$p = $this->find($parent, $start);
$q = $this->find($parent, $end);
return $p == $q;
}
protected function find($parent, $f)
{
while (isset($parent[$f])) {
$f = $parent[$f];
}
return $f;
}
其实就是对照原理将其转化为代码,参照原理看代码很好理解,克鲁斯卡尔算法实现代码比普里姆算法实现代码要精简一些,但是理解起来也还是有一定难度的,下面我们参照普里姆算法测试代码编写克鲁斯卡尔算法测试代码:
// 顶点和边数据
$nodes = ['A', 'B', 'C', 'D', 'E', 'F', 'G'];
$edges = [
['A', 'B', 12],
['A', 'F', 16],
['A', 'G', 14],
['B', 'C', 10],
['B', 'F', 7],
['C', 'D', 3],
['C', 'E', 5],
['C', 'F', 6],
['D', 'E', 4],
['E', 'F', 2],
['E', 'G', 8],
['F', 'G', 9],
];
// 构造无向连通网
$graph = new EdgeWeightedGraph(count($nodes));
foreach ($nodes as $i => $v) {
$graph->addVertex($i, $v);
}
foreach ($edges as $edge) {
$start = $graph->getPosition($edge[0]);
$end = $graph->getPosition($edge[1]);
$graph->addEdge($start, $end, $edge[2]);
}
// 构建并打印最小生成树
$graph->kruskal();
测试结果和之前普里姆算法运行结果完全一样(不一样就是有问题了):

复杂度分析
克鲁斯卡尔算法时间复杂度主要消耗在对边的遍历和回路校验上,假设图的边数是 e,则对应的时间复杂度是 O(eloge),e是指边的循环遍历次数,loge指的是isLoop函数,尤其是 find 函数的时间复杂度,关于这种形式的while循环其实是个递归,所以对应时间复杂度是loge。单从数量级上看克鲁斯卡尔算法要优于普里姆算法。