图 - 最小生成树的实现算法之普里姆（Prim）算法

- 4 mins
PHP 数据结构与算法 图

数据结构与算法系列（四十八）

算法定义

简单来说，普里姆算法从图中某个顶点开始，将其作为一棵树的根节点，然后这棵树会逐步长大，一直长大到覆盖图中的每一个顶点为止，每一步都会从剩下的与当前操作节点相邻的顶点中找到一条权重最小的边加入到树中，当算法终止时，这棵树就是一棵最小生成树。

下面是图示过程：

img

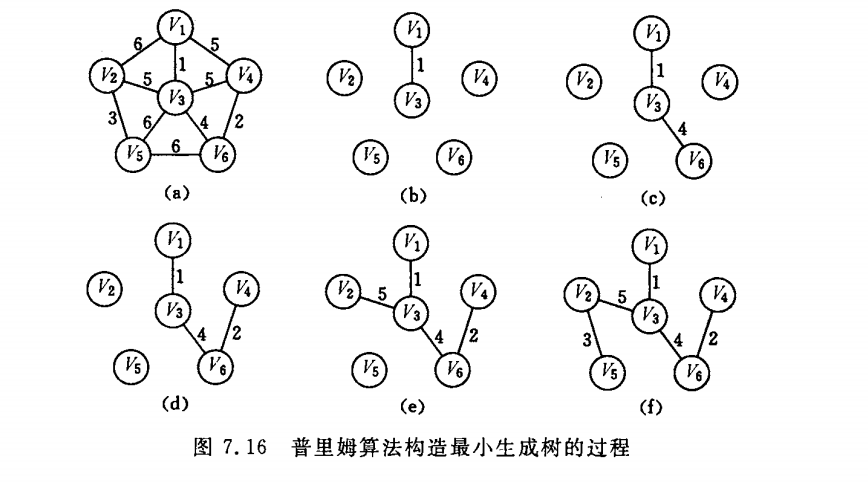
从 V1 开始，从与其相邻的顶点中找到权重最小的边，连接的是 V3，然后从 V3 开始，在于 V3 相邻的顶点中找到权重最小的边，连接的是 V6，再从 V6 开始，依次类推，当到达某个顶点，与该顶点相邻的所有顶点都已经访问过，则需要往前回溯，从所有前驱节点中找到权重最小的一条未添加的边开始，继续上述流程，直到所有顶点都已经覆盖，此时，通过 n-1 条边连接 n 个顶点构成的树就是最小生成树。

算法实现

了解了普里姆算法的原理，接下来，我们就要通过代码来实现它。

在开始编写实现代码之前，需要做一些准备工作，因为最小生成树操作的图的边是有权重的，所以我们需要先构建一个带权重的图，此外，还需要对之前通过邻接表存储图的代码做一些扩展，因为之前保存的无向图是没有权重的，我们将邻接表中存储顶点节点和边节点的节点类分开加以区分：

/**
 * 带权重的边节点
 * Class ENode
 */
class ENode extends Node
{
    public $weight;  // 边的权重值

    public function __construct($data, $weight)
    {
        $this->weight = $weight;
        parent::__construct($data);
    }
}

/**
 * 顶点
 * Class VNode
 */
class VNode extends Node
{

}

对于存储图的邻接链表类也要稍作调整，将属性改成受保护的，以便可以在子类中继承，然后修改插入节点方法如下：

/**
 * Class LinkedList
 * 链表类
 */
class LinkedList
{
    protected $head = null;
    protected $count = 0;

    ...

    public function insert(Node $node)
    {
        if ($this->head == null) {
            return;
        }
        $node->next = $this->head->next;
        $this->head->next = $node;
        $this->count++;
    }

    ...

接下来，我们在最小生成树对应的无向连通网中，继承这个链表类，并新增插入顶点节点和边节点的方法：

/**
 * 邻接链表类
 * Class AdjLinkedList
 */
class AdjLinkedList extends LinkedList
{
    // 插入顶点节点
    public function insertVNode(VNode $node)
    {
        $this->insert($node);
    }

    // 插入边节点
    public function insertENode(ENode $node)
    {
        // 顶点不能为空
        if ($this->head == null || $this->head->next == null) {
            return;
        }
        $vNode = $this->head->next;
        $node->next = $vNode->next;
        $vNode->next = $node;
        $this->count++;
    }
}

最后，我们基于以上数据结构完成无向连通网类 EdgeWeightedGraph 的构建：

/**
 * 无向连通网类
 * Class EdgeWeightedGraph
 */
class EdgeWeightedGraph
{
    private $vNum;  // 顶点总数
    private $vData = []; // 顶点数组
    /**
     * @var AdjLinkedList[]
     */
    private $adj = [];  // 邻接表

    public function __construct($vNum)
    {
        $this->vNum = $vNum;
        for ($i = 0; $i < $vNum; $i++) {
            $this->adj[$i] = new AdjLinkedList();
        }
    }

    // 添加顶点
    public function addVertex($i, $v)
    {
        $vNode = new VNode($v);
        $this->vData[$i] = $v;
        $this->adj[$i]->insertVNode($vNode);
    }

    // 添加边
    public function addEdge($s, $t, $weight)
    {
        $esNode = new ENode($s, $weight);
        $etNode = new ENode($t, $weight);
        $this->adj[$s]->insertENode($etNode);
        $this->adj[$t]->insertENode($esNode);
    }

    /*
     * 获取边<start, end>的权值；若start和end不是连通的，则返回无穷大。
     */
    public function getWeight($start, $end)
    {
        if ($start == $end) {
            return 0;
        }

        $node = $this->adj[$start]->get(0)->next;
        while ($node != null) {
            if ($end == $node->data) {
                return $node->weight;
            }
            $node = $node->next;
        }

        return INF;  // 如果没有找到结束节点返回无限大
    }

    /**
     * 返回指定顶点的位置
     * @param $data
     * @return int
     */
    public function getPosition($data)
    {
        for ($i = 0; $i < $this->vNum; $i++) {
            if ($this->vData[$i] == $data) {
                return $i;
            }
        }
        return -1;
    }
}

在这个类中，我们还是通过邻接表来存储图，在构造函数中对图进行初始化，然后通过 addVNode 在邻接表中添加顶点节点，并且通过额外的 $vData 数组存储顶点数据，通过 addENode 方法向邻接表中插入边节点。此外，我们还提供了 getWeight方法用于获取两个顶点之间边的权重，以及 getPosition 方法获取指定顶点在邻接表中的位置。

有了以上准备工作后，我们就可以正式在上述 EdgeWeightedGraph 类中编写最小生成树的普里姆（Prim）算法实现代码了，其实就是将上面的算法原理做一个转化：

// 通过 Prim 算法实现最小生成树
public function prim($start = 0)
{
    $index = 0;     // prim最小树的索引，即prims数组的索引
    $primTree = [];    // prim最小树的结果数组（顶点）
    $weights = [];  // 顶点间边的权值数组

    // 假设从顶点数组索引start开始构造最小生成树
    $primTree[$index++] = $this->vData[$start];

    // 初始化"顶点的权值数组"，
    // 将每个顶点的权值初始化为"起始顶点start"到"该顶点"的权值。
    for ($i = 0; $i < $this->vNum; $i++ ) {
        $weights[$i] = $this->getWeight($start, $i);
    }

    // 构造最小生成树顶点数组
    for ($i = 0; $i < $this->vNum; $i++) {
        // 由于从 start 开始，所以跳过 start 顶点
        if ($i == $start) {
            continue;
        }

        $j = 0;
        $k = 0;
        $min = INF;   // 初始化最小权值为无穷大
        // 在未被加入到最小生成树的顶点中，找出边权值最小的那个顶点
        while ($j < $this->vNum) {
            if ($weights[$j] != 0 && $weights[$j] < $min) {
                $min = $weights[$j];  // 最小权重值
                $k = $j;   // 对应顶点下标
            }
            $j++;
        }

        // 经过上面的处理后，在未被加入到最小生成树的顶点中，权值最小的顶点是第k个顶点。
        // 将第k个顶点加入到最小生成树的结果数组中
        $primTree[$index++] = $this->vData[$k];
        // 将"第k个顶点的权值"标记为0，意味着该顶点已经加入到最小树结果中
        $weights[$k] = 0;
        // 当第k个顶点被加入到最小生成树的结果数组中之后，以顶点k为起点更新其与其它顶点的权值。
        for ($j = 0 ; $j < $this->vNum; $j++) {
            // 获取第k个顶点到第j个顶点的权值
            $tmp = $this->getWeight($k, $j);
            // 当第j个节点还没有添加到最小生成树，并且权值比之前小时才被更新。
            if ($weights[$j] != 0 && $tmp < $weights[$j]) {
                $weights[$j] = $tmp;
            }
        }
    }

    // 计算最小生成树的权值和
    $sum = 0;
    // 跳过起始顶点
    for ($i = 1; $i < $index; $i++) {
        $min = INF;
        // 获取$primTree[$i]在邻接表中的位置
        $n = $this->getPosition($primTree[$i]);
        // 在$vData[0...i]中，找出到j的权值最小的顶点。
        for ($j = 0; $j < $i; $j++) {
            $m = $this->getPosition($primTree[$j]);
            $tmp = $this->getWeight($m, $n);
            if ($tmp < $min) {
                $min = $tmp;
            }
        }
        $sum += $min;
    }

    // 打印最小生成树
    printf("PRIM(%s)=%d: ", $this->vData[$start], $sum);
    for ($i = 0; $i < $index; $i++) {
        printf("%s ", $primTree[$i]);
    }
}

代码测试

我们可以为上述最小生成树实现代码编写一段简单的测试代码：

// 顶点和边数据
$nodes = ['A', 'B', 'C', 'D', 'E', 'F', 'G'];
$edges = [
    ['A', 'B', 12],
    ['A', 'F', 16],
    ['A', 'G', 14],
    ['B', 'C', 10],
    ['B', 'F',  7],
    ['C', 'D',  3],
    ['C', 'E',  5],
    ['C', 'F',  6],
    ['D', 'E',  4],
    ['E', 'F',  2],
    ['E', 'G',  8],
    ['F', 'G',  9],
];

// 构造无向连通网
$graph = new EdgeWeightedGraph(count($nodes));
foreach ($nodes as $i => $v) {
    $graph->addVertex($i, $v);
}
foreach ($edges as $edge) {
    $start = $graph->getPosition($edge[0]);
    $end = $graph->getPosition($edge[1]);
    $graph->addEdge($start, $end, $edge[2]);
}

// 构造并打印最小生成树结果
$graph->prim();

执行测试代码，输出结果如下：

PRIM(A)=36: A B F E D C G

表明最小生成树构建成功。

算法复杂度

通过分析上述实现代码，很容易看出对于顶点数为 n 的无向连通网，普里姆算法实现最小生成树对应的时间复杂度是 O(n2)（嵌套循环，舍弃低阶对边的遍历），还需要额外的空间存储顶点和边，对应的空间复杂度是 O(n+e)，其中，n 是顶点数，e是边数。

Related Posts

rss facebook twitter github gitlab youtube mail spotify lastfm instagram linkedin google google-plus pinterest medium vimeo stackoverflow reddit quora quora