图 - 最短路径的定义及实现算法(一)
- 4 mins数据结构与算法系列(五十)
最短路径
在日常生活中,我们经常面临路径选择的问题,比如从杭州到北京,可以选择汽车、火车、飞机,甚至还可以坐公交车(这不是笑话,最近网上就流传一个从杭州回临沂,转了35班公交车,行程660多公里,历时7天的神奇春运回家路),对于不同的选择,意味着不同的路径,不同的路径意味着不同的成本,这个成本有时间成本,也有经济成本,不差钱的可以选择时间成本低的,比如坐飞机,经济不那么宽裕却有时间的,可以做公交车,我们把杭州和北京看作图上的两个顶点(中间可能会经过其它城市,即多个顶点),把时间成本或者经济成本看作权重,那么从杭州到北京的路径规划就可以抽象为今天我们要分享的话题 —— 图的最短路径问题。
对于带权重的网图来说,所谓最短路径,指的是两个顶点之间经过的边上权值之和最小的路径,我们将第一个顶点叫做起点,最后一个顶点叫做终点。
最短路径的实现也有多种算法,和最小生成树一样,这里分享两种最常见的实现算法:迪杰斯特拉(Dijkstra)算法和弗洛伊德(Floyd)算法。
迪杰斯特拉算法
迪杰斯特拉(Dijkstra)算法是典型的单源最短路径算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
我们以下面这个无向图为例:
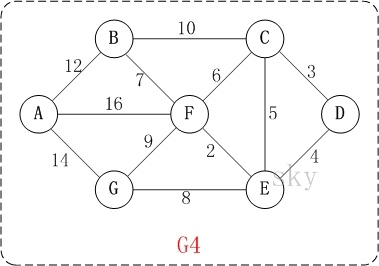
通过迪杰斯特拉算法计算最短路径,需要指定起点,我们用 S 表示图的所有顶点集合,U 表示起点外的其它顶点集合,顶点到自身的距离为0,到相邻顶点距离为相应边的权值,到不相邻顶点的距离为无穷大(∞)。每一次从 U 中找出路径最短的顶点,并将其加入到 S 中,然后,更新 U 中的剩余顶点和顶点对应的路径,重复该操作,直到遍历完所有顶点:
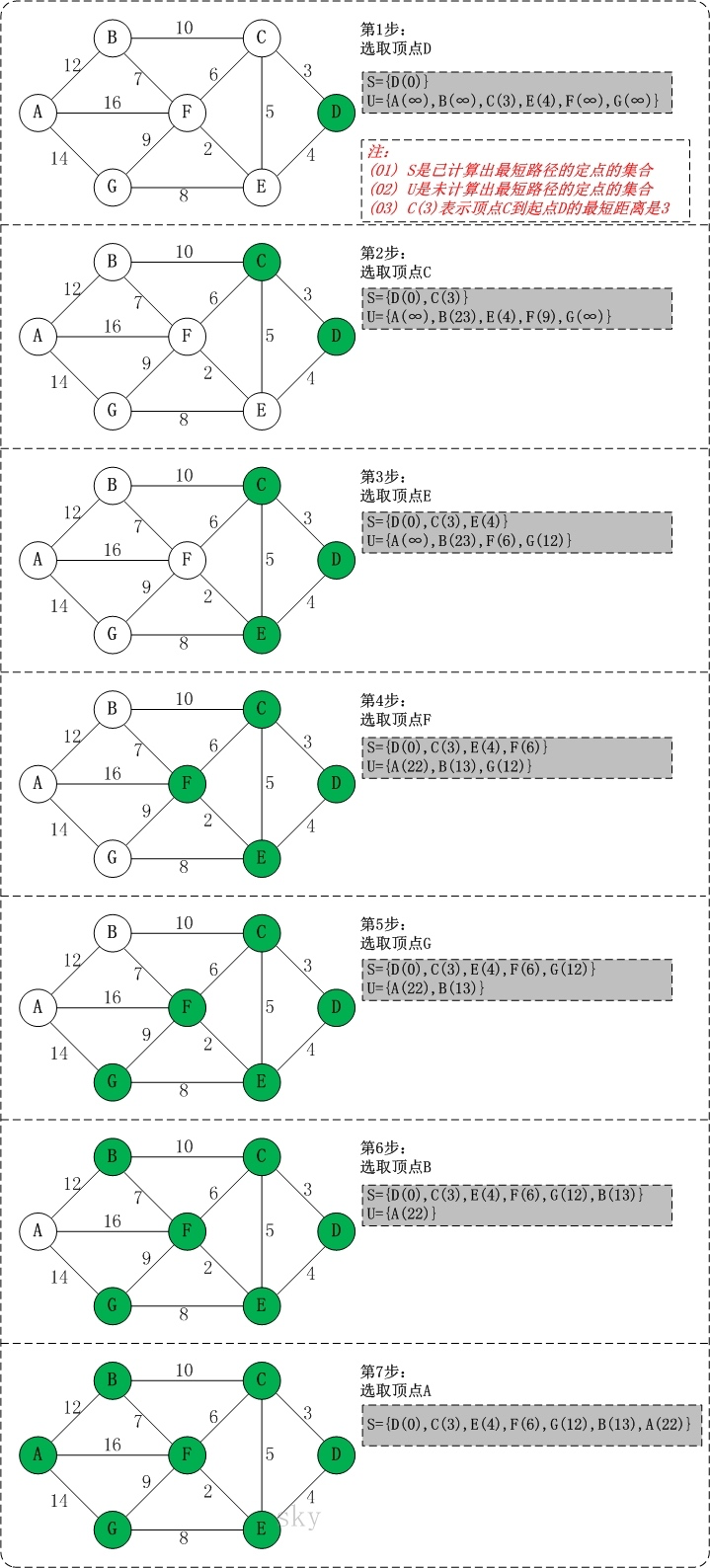
然后我们将上述算法实现思路转化为代码,还是以前面创建的无向网图类 EdgeWeightedGraph 类为基础,在其中编写迪杰斯特拉算法实现方法如下:
// 通过迪杰斯特拉算法实现最短路径
public function dijkstra($start)
{
$prev = []; // 前驱顶点数组,prev[i]的值是起点到顶点i的最短路径所经历的全部顶点中,i之前的那个顶点。
$dist = []; // 长度数组,dist[i]是起点到顶点i的最短路径的长度
$flag = []; // flag[i] = true 表示起点到顶点 i 的最短路径获取成功
// 初始化
for ($i = 0; $i < $this->vNum; $i++) {
$flag[$i] = false;
$prev[$i] = 0;
$dist[$i] = $this->getWeight($start, $i);
}
// 起点
$flag[$start] = true;
$dist[$start] = 0;
// 遍历图,每次找出一个顶点的最短路径。
$k = 0;
for ($i = 1; $i < $this->vNum; $i++) {
// 在未获取最短路径的顶点中,找到离起点最近的顶点(k)。
$min = INF;
for ($j = 0; $j < $this->vNum; $j++) {
if ($flag[$j] == false && $dist[$j] < $min) {
$min = $dist[$j];
$k = $j;
}
}
// 标记顶点k为已经获取到最短路径
$flag[$k] = true;
// 当获取顶点k的最短路径之后,更新未获取最短路径的顶点的最短路径和前驱顶点。
for ($j = 0; $j < $this->vNum; $j++) {
$tmp = ($this->getWeight($k, $j) == INF ? INF : ($min + $this->getWeight($k, $j)));
if ($flag[$j] == false && ($tmp < $dist[$j])) {
$dist[$j] = $tmp;
$prev[$j] = $k;
}
}
}
// 打印dijkstra最短路径的结果
printf("dijkstra(%s): \n", $this->vData[$start]);
for ($i = 0; $i < $this->vNum; $i++) {
printf(" shortest(%s, %s)=%d\n", $this->vData[$start], $this->vData[$i], $dist[$i]);
}
}
迪杰斯特拉算法会以某个顶点为起点,计算该顶点到图中所有其它顶点的最短路径,我们为其编写测试代码如下:
// 顶点和边数据
$nodes = ['A', 'B', 'C', 'D', 'E', 'F', 'G'];
$edges = [
['A', 'B', 12],
['A', 'F', 16],
['A', 'G', 14],
['B', 'C', 10],
['B', 'F', 7],
['C', 'D', 3],
['C', 'E', 5],
['C', 'F', 6],
['D', 'E', 4],
['E', 'F', 2],
['E', 'G', 8],
['F', 'G', 9],
];
// 构造无向连通网
$graph = new EdgeWeightedGraph(count($nodes));
foreach ($nodes as $i => $v) {
$graph->addVertex($i, $v);
}
foreach ($edges as $edge) {
$start = $graph->getPosition($edge[0]);
$end = $graph->getPosition($edge[1]);
$graph->addEdge($start, $end, $edge[2]);
}
// 计算并打印最短路径
$graph->dijkstra($graph->getPosition('A'));
执行测试代码,输出结果如下:

表明最短路径计算无误。
最后,我们简单分析下迪杰斯特拉算法的时间复杂度,很明显,对于计算某个顶点到任意其它顶点需要两层嵌套循环,对应的时间复杂度是 O(n^2),如果要计算所有顶点的最短路径,则还要在外面嵌套一层循环,对应的时间复杂度是 O(n^3)。当顶点很多,路径很复杂时,对时间开销不小。
下篇文章,我们将分享通过弗洛伊德算法来计算网图的最短路径,看看能否对时间复杂度进行优化。